7.5.2 Dufort-Frankel scheme (1953)
Richardson scheme in (7.57) can be made stable by the following modification: $$ \begin{equation} \tag{7.58} u^n_j=\frac{1}{2}(u_j^{n+1}+u^{n-1}_j) \end{equation} $$
which inserted in (7.57) gives: $$ \begin{equation} \tag{7.59} u^{n+1}_j=\frac{1}{1+2D}\left[ (1-2D)u^{n-1}_j+2D(u^n_{j+1}+u^n_{j-1})\right] \end{equation} $$
This is an explicit 3-level scheme called DuFort-Frankel scheme, see Figure 93.
Figure 93: 3-level stencil of the DuFort-Frankel scheme (7.59).
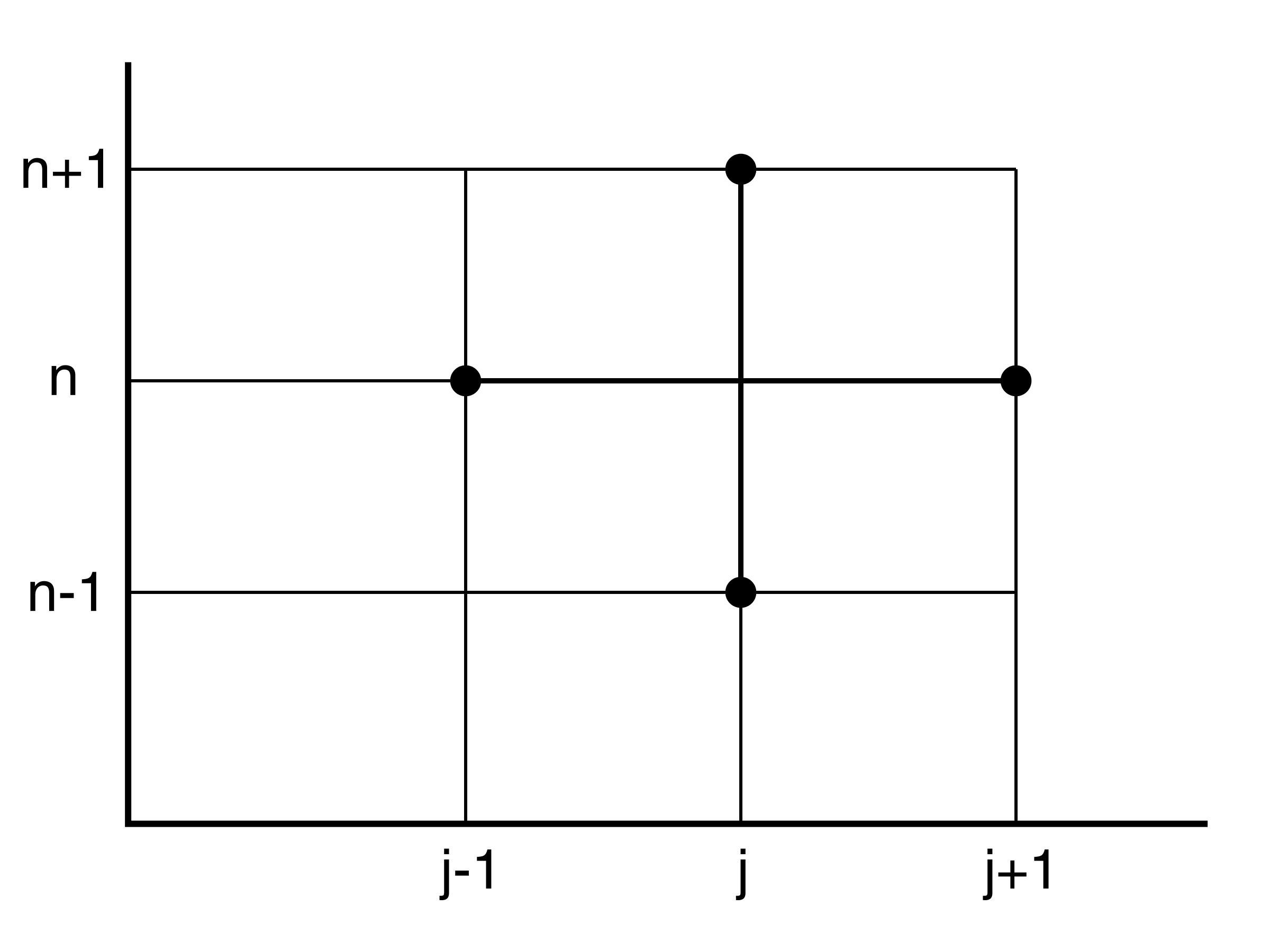
3-level schemes where \( u^n_j \) is missing are called Leap-frog-type schemes for obvious reasons. The sufficient criterion of positive coefficients in (7.21) requires that \( D\leq \frac{1}{2} \) for a stable scheme. The stability analysis here is slightly more complicated as with previous cases because we have to discuss what happens when \( G \) takes complex values.
Inserting (7.42) in (7.59) and division by \( G^{n-1}e^{e^{i\delta j}} \) yields: $$ \begin{equation*} G^2= \frac{1}{1+2r}\left[(1-2r)+2r\cdot G\cdot (e^{i\delta}+e^{-i\delta})\right] = \frac{1}{1+2r}\left[(1-2r)+4r\cdot G\cdot \cos(\delta)\right] \end{equation*} $$ which gives the following 2nd order equation: $$ \begin{equation*} (1+2D)\cdot G^2-4D\cdot G\cos(\delta)-(1-2D)=0\,, \end{equation*} $$ with roots: $$ \begin{equation*} \begin{array}{lcl} G_{1,2} & = & \dfrac{4D\cos(\delta) \pm \sqrt{(4D\cos(\delta))^2 +4(1+2D)\cdot(1-2D)}}{2(1+2D)}\\ & = & \dfrac{2D\cos(\delta)\pm \sqrt{1-D^2\sin^2(\delta)}}{1+2D}. \end{array} \end{equation*} $$
For stability, both roots must meet the condition \( |G|\leq 1 \). In general, we must distinguish between real and complex roots to take care of the case for which \( G\leq 0 \) when \( G \) is real.
- Real roots: \( 1-4D^2\sin(\delta)\geq0 \)
\( |G_{1,2}| \leq \dfrac{2D\cdot |\cos(\delta)|+\sqrt{1-4D^2\sin^2(\delta)}}{1+2r}\leq \dfrac{1+2D}{1+2D}\leq1 \)
- Complex roots: \( 1-4D^2\sin^2(\delta) < 0 \to \sqrt{1-4D^2\sin^2(\delta)}=i\cdot \sqrt{4D^2\sin^2(\delta)-1} \)
\( |G_{1,2}|^2= \bigg|\frac{\big(2D\cos(\delta)\big)^2+4D^2\sin^2(\delta)-1}{(1+2D)^2}\bigg|=\bigg|\frac{4D^2-1}{4D^2+4D+1}\bigg|=\bigg|\frac{2D-1}{2D+1}\bigg| < 1 \)